Después de mucho tiempo sin publicar entrada alguna y dejando algo abandonado este blog, volvemos a actualizarlo con una nueva edición del concurso de ingenio de nuestro IES. Ahí os lo dejo:
25/04/2014
21/11/2013
El coeficiente de Gini como medida de la desigualdad
El coeficiente de Gini es una medida de la desigualdad ideada por el estadístico italiano Corrado Gini. Normalmente se utiliza para medir la desigualdad en los ingresos, dentro de un país, pero puede utilizarse para medir cualquier forma de distribución desigual. El coeficiente de Gini es un número entre 0 y 1, en donde 0 se corresponde con la perfecta igualdad (todos tienen los mismos ingresos) y donde el valor 1 se corresponde con la perfecta desigualdad (una persona tiene todos los ingresos y los demás ninguno).
En la siguiente imagen, podemos ver la distribución de este índice por países:
El coeficiente de Gini se calcula como una proporción de las áreas en el diagrama de la curva de Lorenz. Si el área entre la línea de perfecta igualdad y la curva de Lorenz es a, y el área por debajo de la curva de Lorenz es b, entonces el coeficiente de Gini es a/(a+b).
Esta proporción se expresa como porcentaje o como equivalente numérico de ese porcentaje, que es siempre un número entre 0 y 1. El coeficiente de Gini se calcula a menudo con la Fórmula de Brown, que es más práctica:
Donde:
- G: Coeficiente de Gini
- X: Proporción acumulada de la variable población
- Y: Proporción acumulada de la variable ingresos
De forma resumida, la Curva de Lorenz es una gráfica de concentración acumulada de la distribución de la riqueza superpuesta a la curva de la distribución de frecuencias de los individuos que la poseen, y su expresión en porcentajes es el índice de Gini.
21/06/2013
El Tres en Raya definitivo
¿Quién no ha jugado nunca al Tres en Raya? Es uno de los juegos más famosos y jugados de todo el mundo. Sin embargo, con la práctica se convierte en un juego aburrido, sujeto a pocas sorpresas, que no exige demasiada estrategia y que, bien jugado por parte de los jugadores, casi siempre acaba en tablas.
Para evitar este problema, tenemos la siguiente versión, un Tres en Raya recurrente, el definitivo. Se juega en nueve tableros que, a su vez, forman un tablero mayor. Cada jugador está obligado a jugar en el tablero cuya posición determine el último movimiento realizado por su contrincante. Gana el jugador que consiga vencer en tres tableros que formen a su vez una línea horizontal, vertical o diagonal.
He jugado un par de partidas y la verdad es que engancha. Puede descargarse como aplicación gratuita para Android en el siguiente enlace.
19/06/2013
El Bueno de Cuttlas y las matemáticas
Cuttlas (o El Bueno de Cuttlas) es un muñeco minimalista concebido con trazos simples y estilo naïf, protagonista de una tira cómica dibujada por Eduardo Pelegrín Martínez de Pisón, más conocido como Calpurnio, historietista y animador español, nacido en Zaragoza en 1959.
El vaquero Cuttlas nos habla de sus inquietudes y aventuras desde un punto de vista ora realista, ora metafísico meditando sobre la existencia, las relaciones humanas, el arte y, como no, las matemáticas.
12/04/2013
Concurso de Ingenio del IES Antonio de Nebrija 2012/2013
Aquí tenéis, otro año más, el solucionario del concurso de ingenio de este año. Espero que se os haya dado bien.
23/01/2013
Cómo quitarse el chaleco sin quitarse la chaqueta
Hace un año, realizamos una entrada explicando cómo realizar un nudo en una cuerda sin soltar sus extremos. Lo que parecía ser magia, era en realidad, topología. En el siguiente vídeo, Fernando Blasco, nos enseña un truco similar, cómo deshacernos de un chaleco sin quitarnos previamente la chaqueta, también relacionado con esta rama de las matemáticas, y dando respuesta así a un reto lanzado desde el blog Grado 361, de la Cadena Ser.
19/12/2012
Sociogramas: Matrices y grafos para la mejora de la convivencia escolar
Un sociograma es, para que nos entendamos, una radiografía de las relaciones que se establecen en un grupo, es decir, una representación gráfica de estas relaciones, poniendo así de manifiesto los lazos de influencia y de preferencia que existen en el mismo.
Como docentes, y para mejorar nuestra labor de gestor de un grupo más o menos diverso, podemos ayudarnos de la elaboración de un sociograma de aula. Es una práctica muy común y útil en la detección de posibles líderes, alumnos poco integrados o subgrupos cerrados dentro del grupo-clase.
Para la elaboración de un sociograma de aula, bastaría con preguntar a cada alumno cuáles son sus tres mejores amigos dentro del grupo, a cuáles elegiría para pasar una tarde divertida o para realizar un viaje. Con sus respuestas, podemos elaborar un grafo como el siguiente:
Cada nodo del grafo representa a un alumno del grupo y cada flecha una relación de afinidad o amistad declarada por el emisor de esa flecha. Aunque la información mostrada sea abundante, de un solo vistazo se pueden extraer ya ciertas conclusiones. Yo, además, me he permitido el colorear de forma distinta a los chicos de las chicas y el realizar un recuento que he anotado al lado de cada nodo, por si podía sacar a la luz algo interesante relacionado con cada uno de estos dos subgrupos.
Como todo grafo, toda la información contenida en un sociograma se puede almacenar en una matriz, que es un elemento más manejable, más computable. Ésta es la matriz de adyacencia: una matriz cuadrada cuyo orden lo proporciona el número de nodos (alumnos) y compuesta por ceros y unos.
Con un ejemplo arrojaremos algo de luz a este concepto. El siguiente grafo refleja las relaciones de amistad entre cuatro alumnos:
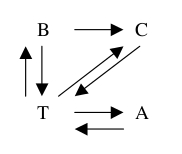La matriz de adyacencia asociada establece con unos o ceros cada una de las posibles relaciones que se pueden establecer entre estos cuatro alumnos. Para este caso en concreto, su matriz de adyacencia es la siguiente:
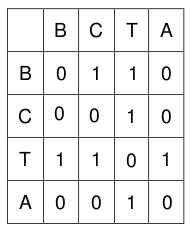Evidentemente, para un ejemplo real como el que mostramos anteriormente, la matriz de adyacencia sería mucho más grande, nada menos que una matriz de tamaño 24×24, pero compuesta por ceros y unos, lo que la hace totalmente computable.
La potencia de esta representación en el estudio de las relaciones personales dentro de un grupo es tremenda. Como muestra, un botón: la potencia enésima de la matriz de adyacencia determina el número de relaciones «amigo de un amigo de un amigo… (n veces) … de un amigo» que se pueden establecer entre cada par de componentes de este grupo.
03/12/2012
MATEMÁTICAS DE CERCA: Ni un día sin leer, ni un día sin pensar
Matemáticas de Cerca es una colección de láminas divulgativas que desde el curso 2006/07 está realizando el Grupo Alquerque de Sevilla. La intención es proporcionar a los centros educativos, y en particular al profesorado de matemáticas, un recurso didáctico para abordar temáticas complementarias a las tratadas en el currículo.
Su lema es «Ningún día sin leer, ningún día sin pensar», pues considerando el valor de la lectura insustituible, y más en la actual sociedad de la comunicación, para convertir información en conocimiento, se pretende incorporar la matemática, el razonamiento, para formar lectores competentes en el uso de los distintos textos y para despertar el interés por la lectura matemática como medio de conocimiento y placer.
Los temas que se abordan son muy diversos, por ello se han estructurado en bloques: números, desafíos, literatura, juegos, magia, geometría, humor, etc…
El diseño es común a todas las láminas con la intención de crear una imagen reconocida y uniforme. A la vez, estas láminas son también un recurso que facilita divulgar las matemáticas entre el alumnado y el profesorado. Su formato permite la utilización tanto individual como expositiva, para colocar en pasillos, tablones de anuncios, aulas…
04/10/2012
27/06/2012
Imagina un mundo sin matemáticas… Save The Children
«Imagina un mundo sin matemáticas. Así es. No hay manera de calcular tu promedio de bateo o de estimar el número de tus seguidores en Twitter…»
A World with No Math es una campaña de la ONG Save the Children protagonizada por Michael Boatman -Anger Management-, Julie Bowman -Modern Family-, Simon Helberg -The Big Bang Theory- y John Oliver -The Daily Show with Jon Stewart-.
La ONG quiere llamar la atención con esta campaña sobre las carencias de las niñas y los niños en los países pobres. Su proyecto Numeracy Boost es un programa de educación centrado en enseñar a niñas y niños -en principio de Bangladesh y Malawi- las habilidades matemáticas básicas que necesitan para prosperar en la vida cotidiana pasando por contar ganado hasta calcular el momento de la época de lluvias. Al aumentar las habilidades matemáticas de niñas y niños, se les prepara para tener más oportunidades en la escuela y la vida.
MATEMATES 